TA的每日心情 | 开心
2013-3-3 12:12 |
|---|
签到天数: 82 天 [LV.6]常住居民II
|

楼主 |
发表于 2016-1-6 11:22:39
|
显示全部楼层
本帖最后由 smartdou 于 2016-1-6 11:26 编辑
一维热传导方程的格林函数解及其它
Some Green's function solutions in 1D[edit]
A variety of elementary Green's function solutions in one-dimension are recorded here; many others are available elsewhere.[8] In some of these, the spatial domain is (−∞,∞). In others, it is the semi-infinite interval (0,∞) with either Neumann or Dirichlet boundary conditions. One further variation is that some of these solve the inhomogeneous equation
 where f is some given function of x and t. where f is some given function of x and t.

Homogeneous heat equation[edit]Initial value problem on (−∞,∞)
 Comment. This solution is the convolution with respect to the variable x of the fundamental solution Comment. This solution is the convolution with respect to the variable x of the fundamental solution

and the function g(x). Therefore, according to the general properties of the convolution with respect to differentiation, u = g ∗ Φ is a solution of the same heat equation, for

Moreover,
 
so that, by general facts about approximation to the identity, Φ(⋅, t) ∗ g → g as t → 0 in various senses, according to the specific g. For instance, if g is assumed bounded and continuous on R then Φ(⋅, t) ∗ g converges uniformly to g as t → 0, meaning that u(x, t) is continuous on R × [0, ∞) with u(x, 0) = g(x).


Initial value problem on (0,∞) with homogeneous Dirichlet boundary conditionsComment.
This solution is obtained from the preceding formula as applied to the data g(x) suitably extended to R, so as to be an odd function, that is, letting g(−x) := −g(x) for all x. Correspondingly, the solution of the initial value problem on (−∞,∞) is an odd function with respect to the variable x for all values of t, and in particular it satisfies the homogeneous Dirichlet boundary conditions u(0, t) = 0.
Initial value problem on (0,∞) with homogeneous Neumann boundary conditions

Comment.
This solution is obtained from the first solution formula as applied to the data g(x) suitably extended to R so as to be an even function, that is, letting g(−x) := g(x) for all x. Correspondingly, the solution of the initial value problem on R is an even function with respect to the variable x for all values of t > 0, and in particular, being smooth, it satisfies the homogeneous Neumann boundary conditions ux(0, t) = 0.
Problem on (0,∞) with homogeneous initial conditions and non-homogeneous Dirichlet boundary conditions 0" src="https://upload.wikimedia.org/math/d/4/5/d45f775cdeb0b0eb572bf27e28e5f4de.png">Comment. 0" src="https://upload.wikimedia.org/math/d/4/5/d45f775cdeb0b0eb572bf27e28e5f4de.png">Comment.
This solution is the convolution with respect to the variable t of

and the function h(t). Since Φ(x, t) is the fundamental solution of
 the function ψ(x, t) is also a solution of the same heat equation, and so is u := ψ ∗ h, thanks to general properties of the convolution with respect to differentiation. Moreover, the function ψ(x, t) is also a solution of the same heat equation, and so is u := ψ ∗ h, thanks to general properties of the convolution with respect to differentiation. Moreover,
 
so that, by general facts about approximation to the identity, ψ(x, ⋅) ∗ h → h as x → 0 in various senses, according to the specific h. For instance, if h is assumed continuous on R with support in [0, ∞) then ψ(x, ⋅) ∗ h converges uniformly on compacta to h as x → 0, meaning that u(x, t) is continuous on [0, ∞) × [0, ∞) with u(0, t) = h(t).
Inhomogeneous heat equation[edit]Problem on (-∞,∞) homogeneous initial conditions
Comment.
This solution is the convolution in R2, that is with respect to both the variables x and t, of the fundamental solution
 and the function f(x, t), both meant as defined on the whole R2 and identically 0 for all t → 0. One verifies that

which expressed in the language of distributions becomes

where the distribution δ is the Dirac's delta function, that is the evaluation at 0.
Problem on (0,∞) with homogeneous Dirichlet boundary conditions and initial conditions
Comment.
This solution is obtained from the preceding formula as applied to the data f(x, t) suitably extended to R × [0,∞), so as to be an odd function of the variable x, that is, letting f(−x, t) := −f(x, t) for all x and t. Correspondingly, the solution of the inhomogeneous problem on (−∞,∞) is an odd function with respect to the variable x for all values of t, and in particular it satisfies the homogeneous Dirichlet boundary conditions u(0, t) = 0.
Problem on (0,∞) with homogeneous Neumann boundary conditions and initial conditions
Comment. This solution is obtained from the first formula as applied to the data f(x, t) suitably extended to R × [0,∞), so as to be an even function of the variable x, that is, letting f(−x, t) := f(x, t) for all x and t. Correspondingly, the solution of the inhomogeneous problem on (−∞,∞) is an even function with respect to the variable x for all values of t, and in particular, being a smooth function, it satisfies the homogeneous Neumann boundary conditions ux(0, t) = 0.
Examples[edit]Since the heat equation is linear, solutions of other combinations of boundary conditions, inhomogeneous term, and initial conditions can be found by taking an appropriate linear combination of the above Green's function solutions.
For example, to solve

let u = w + v where w and v solve the problems

Similarly, to solve

let u = w + v + r where w, v, and r solve the problems

Mean-value property for the heat equation[edit]
Solutions of the heat equations

satisfy a mean-value property analogous to the mean-value properties of harmonic functions, solutions of
 , ,
though a bit more complicated. Precisely, if u solves

and

then

where Eλ is a "heat-ball", that is a super-level set of the fundamental solution of the heat equation:
\lambda\}," src="https://upload.wikimedia.org/math/4/1/f/41f0f80fbb38f91398ced52c14533de0.png">
Notice that
 as λ → ∞ so the above formula holds for any (x, t) in the (open) set dom(u) for λ large enough. Conversely, any function u satisfying the above mean-value property on an open domain of Rn × R is a solution of the heat equation. This can be shown by an argument similar to the analogous one for harmonic functions. as λ → ∞ so the above formula holds for any (x, t) in the (open) set dom(u) for λ large enough. Conversely, any function u satisfying the above mean-value property on an open domain of Rn × R is a solution of the heat equation. This can be shown by an argument similar to the analogous one for harmonic functions.
Stationary heat equation[edit]
The (time) stationary heat equation is not dependent on time. In other words, it is assumed conditions exist such that:

This condition depends on the time constant and the amount of time passed since boundary conditions have been imposed. Thus, the condition is fulfilled in situations in which the time equilibrium constant is fast enough that the more complex time-dependent heat equation can be approximated by the stationary case. Equivalently, the stationary condition exists for all cases in which enough time has passed that the thermal field u no longer evolves in time.
In the stationary case, a spatial thermal gradient may (or may not) exist, but if it does, it does not change in time. This equation therefore describes the end result in all thermal problems in which a source is switched on (for example, an engine started in an automobile), and enough time has passed for all permanent temperature gradients to establish themselves in space, after which these spatial gradients no longer change in time (as again, with an automobile in which the engine has been running for long enough). The other (trivial) solution is for all spatial temperature gradients to disappear as well, in which case the temperature become uniform in space, as well.
The equation is much simpler and can help to understand better the physics of the materials without focusing on the dynamic of the heat transport process. It is widely used for simple engineering problems assuming there is equilibrium of the temperature fields and heat transport, with time.
Stationary condition:

The stationary heat equation for a volume that contains a heat source (the inhomogeneous case), is the Poisson's equation:
 where u is the temperature, k is the thermal conductivity and q the heat-flux density of the source. where u is the temperature, k is the thermal conductivity and q the heat-flux density of the source.
In electrostatics, this is equivalent to the case where the space under consideration contains an electrical charge.
The stationary heat equation without a heat source within the volume (the homogeneous case) is the equation in electrostatics for a volume of free space that does not contain a charge. It is described by Laplace's equation:

Applications[edit]Particle diffusion[edit]
Main article: Diffusion equation
One can model particle diffusion by an equation involving either:
In either case, one uses the heat equation
 or or

Both c and P are functions of position and time. D is the diffusion coefficient that controls the speed of the diffusive process, and is typically expressed in meters squared over second. If the diffusion coefficient D is not constant, but depends on the concentration c (or P in the second case), then one gets the nonlinear diffusion equation.
Brownian motion[edit]
Let the stochastic process  be the solution of the stochastic differential equation be the solution of the stochastic differential equation

where  is the Wiener process (standard Brownian motion). Then the probability density function of is the Wiener process (standard Brownian motion). Then the probability density function of  is given at any time is given at any time  by by

which is the solution of the initial value problem
 where where 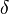 is the Dirac delta function. is the Dirac delta function.
|
|
 |Archiver|手机版|小黑屋|阳光石油网
( 鲁ICP备2021003870号-1 )
|Archiver|手机版|小黑屋|阳光石油网
( 鲁ICP备2021003870号-1 )